Parametric vs. Non-Parametric Tests and When to Use Them

A parametric test makes assumptions while a non-parametric test does not assume anything.

The fundamentals of data science include computer science, statistics and math. It’s very easy to get caught up in the latest and greatest, most powerful algorithms — convolutional neural nets, reinforcement learning, etc.

As an ML/health researcher and algorithm developer, I often employ these techniques. However, something I have seen rife in the data science community after having trained ~10 years as an electrical engineer is that if all you have is a hammer, everything looks like a nail. Suffice it to say that while many of these exciting algorithms have immense applicability, too often the statistical underpinnings of the data science community are overlooked.

What is the Difference Between Parametric and Non-Parametric Tests?

A parametric test makes assumptions about a population’s parameters, and a non-parametric test does not assume anything about the underlying distribution.

I’ve been lucky enough to have had both undergraduate and graduate courses dedicated solely to statistics , in addition to growing up with a statistician for a mother. So this article will share some basic statistical tests and when/where to use them.

A parametric test makes assumptions about a population’s parameters:

1. Normality : Data in each group should be normally distributed.
2. Independence : Data in each group should be sampled randomly and independently.
3. No outliers : No extreme outliers in the data.
4. Equal Variance : Data in each group should have approximately equal variance.

If possible, we should use a parametric test. However, a non-parametric test (sometimes referred to as a distribution free test ) does not assume anything about the underlying distribution (for example, that the data comes from a normal (parametric distribution).

We can assess normality visually using a Q-Q (quantile-quantile) plot. In these plots, the observed data is plotted against the expected quantile of a normal distribution . A demo code in Python is seen here, where a random normal distribution has been created. If the data are normal, it will appear as a straight line.

import numpy as np import statsmodels.api as statmod import matplotlib.pyplot as plt #create dataset with 100 values that follow a normal distribution data = np.random.normal(0,1,100) #create Q-Q plot with 45-degree line added to plot fig = statmod.qqplot(data, line='45') plt.show()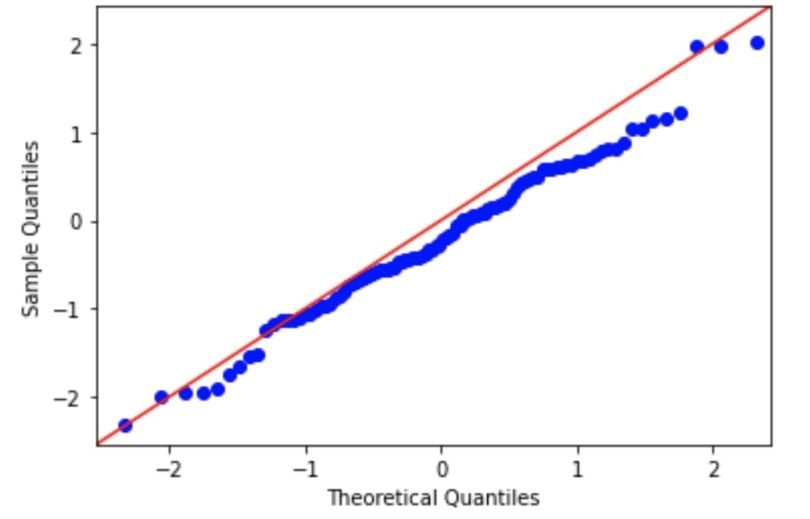

Tests to Check for Normality

• Shapiro-Wilk
• Kolmogorov-Smirnov

The null hypothesis of both of these tests is that the sample was sampled from a normal (or Gaussian) distribution. Therefore, if the p-value is significant, then the assumption of normality has been violated and the alternate hypothesis that the data must be non-normal is accepted as true.

Selecting the Right Test

You can refer to this table when dealing with interval level data for parametric and non-parametric tests.

Advantages and Disadvantages

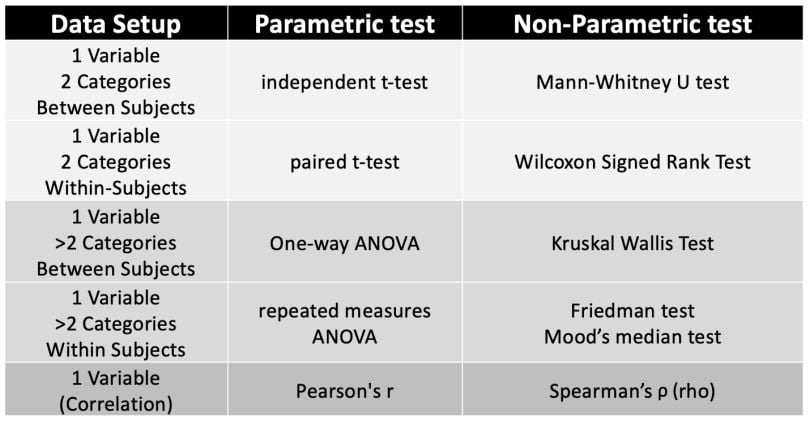
Non-parametric tests have several advantages, including:

• More statistical power when assumptions of parametric tests are violated.
• Assumption of normality does not apply.
• Small sample sizes are okay.
• They can be used for all data types, including ordinal, nominal and interval (continuous).
• Can be used with data that has outliers.

Disadvantages of non-parametric tests:

• Less powerful than parametric tests if assumptions haven’t been violated

References

[2] Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics , Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education

[3] Rumsey, D. J. (2003). Statistics for dummies, 18th edition